SMW Hackings deutsches ASM Tutorial für Anfänger und Fortgeschrittene by Markus Wall also known as RPG Hacker TM
(oder kurz: SMWHdASMTfAuFbMWakaRPGH)
---------------------------------------------------------------------------
LEKTION 1: BINÄRES- UND HEXADEZIMALES ZAHLENSYSTEM
Wie ihr sicherlich alle wisst oder wissen solltet, arbeitet ein Computer mit Einsen und Nullen. Dies nennt man das Binärsystem. Eine Beispielzahl in binär könnte z.B. so aussehen:
00011001
Nun mal grundlegendes zum Binärsytem:
-Die einzelnen "Ziffern" einer binären Zahl nennt man Bits. 8 Bits sind 1 Byte.
-Bei der Benennung der Bits geht man von hinten nach vorne. Das Bit ganz rechts ist Bit 0, eine Stelle weiter links ist Bit 1, noch eine Stelle weiter links ist Bit 2 usw.
-Eine binäre Ziffer kann nur den Wert 1 (set) oder 0 (clear) haben.
Wie aber funktioniert das binäre Zahlensystem nun genau? Ich sag nur ein Wort: Zweierpotenzen!
Jedes Bit einer binären Zahl steht für eine Zweierpotenz, wieder ganz rechts angefangen mit
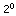 . Nun, ich hoffe ihr habt Mathematik einigermaßen drauf, denn das ist hier echt das Minimum. Aber falls nicht hier noch mal eine Liste:
. Nun, ich hoffe ihr habt Mathematik einigermaßen drauf, denn das ist hier echt das Minimum. Aber falls nicht hier noch mal eine Liste: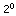 = 1
= 1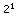 = 2
= 2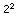 = 4
= 4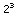 = 8
= 8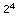 = 16
= 16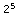 = 32
= 32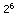 = 64
= 64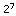 = 128
= 128Falls ihr die Potenzrechnung nicht drauf habt, dann merkt euch einfach, dass jedes Bit doppelt so groß ist, wie das vorherige.
Nun müsst ihr einfach alle gesetzten Bits zusammenzählen. Noch mal das Beispiel von oben: 00011001 (denkt dran, wir gehen von hinten nach vorne):
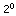 + 0 + 0 +
+ 0 + 0 + 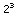 +
+ 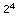 + 0 + 0 + 0
+ 0 + 0 + 0= 1 + 0 + 0 + 8 + 16 + 0 + 0 + 0 = 25
Diese Zahl ist dezimal geschrieben also 25.
Rechnen tut man im Binärsystem genau so wie im Dezimalsystem mit der schriftlichen Addition, bloß, dass man nur zwei Ziffern hat. Also Beispiel:
0110 +
0101
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0; Übertrag: 1
0 + 1 = 1
Das Ergebnis lautet also 1011
Wie ihr seht, kann das ganze hier ziemlich kompliziert und unübersichtlich werden. Genau aus diesem Grund hat man das Hexadezimalsystem entwickelt. Das Hexadezimalsystem funktioniert genau wie das Dezimalsystem, bloß, dass man 16 statt 10 Ziffern hat. Um die fehlenden Ziffern darstellen zu können, nimmt man einfach die Buschstaben A bis F. So ist die höchste Ziffer im Hexadezimalsystem nicht die 9, sondern F (15 in dezimal). Die Addition funktioniert auch hier wieder wie die schriftliche Addition im Dezimalsystem. Also:
1F3B +
2242
B + 2 = D
3 + 4 = 7
F + 2 = 1; Übertrag: 1
1 + 3 = 4
Das Ergebnis dieser Addition ist also 417D.
Das Hexadezimalsystem wird hauptsächlich dazu verwendet, um binäre Zahlen ansehlicher zu machen. So schreibt man statt 11010011 z.B. D3. Noch was wichtiges, was ihr euch merken solltet:
1111 = F = 15
11111111 = FF = 255
1111111111111111 = FFFF = 65535
Ich hoffe mal, dass dies einigermaßen verstanden wurde. Wenn ihr ganz leicht Hexzahlen in Binärzahlen konvertieren wollt oder umgekehrt, müsst ihr einfach folgendes tun (nur für Windows Nutzer):
1. Geht auf Start > Ausführen
2. Gibt ins Feld "calc" ein und klickt dann auf "OK"
3. Geht auf "Ansicht" und danach je nach Betriebssystem auf "Wissenschaftlich" bzw. "Programmierer"
Ihr solltet nun diese Ansicht bekommen:
(Windows XP)

(Windows 7)
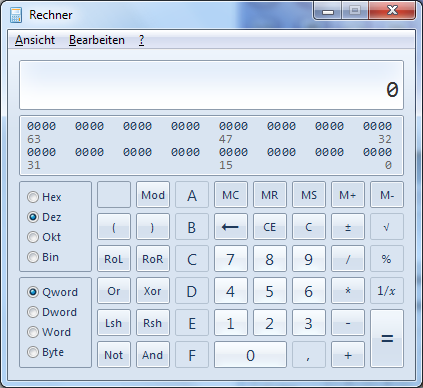
Zuerst wählt ihr oben rechts die Ausgangszahl aus, also z.B. "Hex".
Danach gibt ihr die Zahl ein, die ihr konvertieren wollt.
Danach klickt ihr oben links auf den gewünschten Zahlentyp, also z.B. "Bin".
Das war's schon! Eure Zahl wurde nun erfolgreich konvertiert.
Ich weiß, dass das ganze hier ziemlich kompliziert ist und die meisten von euch vermutlich schon längst abgeschaltet haben, aber das alles hier perfekt zu beherrschen ist einfach Grundvorraussetzung, wenn man es in ASM Programmierung zu etwas bringen will.
---------------------------------------------------------------------------
LEKTION 2: DER ASM GRUNDBEGRIFF
Oben das war alles nur eine Einführung. Nun geht es erst mit der eigentlichen ASM Programmierung los.
Was ist ASM überhaupt?
Nun, ich habe euch oben schon das Binär- und Hexadezimalsystem vorgestellt. Außerdem habe ich erwähnt, dass Computer nur durch Einsen und Nullen laufen. Das gilt auch für SMW. SMW besteht komplett aus Einsen und Nullen. Diese Einsen und Nullen wären aber ziemlich unübersichtlich, deshalb gibt es das Hexadezimalsystem. Assembly erfüllt nun genau die selbe Aufgabe, wie das Hexadezimalsystem: Es macht die Programmierung übersichtlicher. Denn ganz ehrlich: Obwohl das Hexadezimalsystem sehr viel übersichtlicher als das Binärsystem ist, kann man mit Code wie
8D BF 1D....
Noch nicht wirklich viel anfangen. Erstens müsste man sich unzählige Zahlen merken und zweitens ist es einfach sehr schwer, einen gesuchten Wert zu finden. Darum benutzt man ASM. SMW lässt sich also komplett als ASM Code darstellen.
So, das war jetzt die Theorie hinter dem ganzen. Wo ist aber der praktische Nutzen? Ganz einfach: Natürlich lässt sich dieser Code auch verändern, und genau da wird das ganze interessant. Tools wie Lunar Magic, Addmusic, Sprite Tool, Block Tool usw. tun nichts anderes, als diesen Code zu verändern. Meistens bekommt man davon allerdings nicht viel zu sehen. In Lunar Magic z.B. bekommt man nur ein fertiges SMW zu sehen. In Wirklichkeit aber übersetzt Lunar Magic sämtliche Befehle in ASM Code und überschreibt damit den originalen SMW Code. Allerdings ist man hier natürlich and die Funktionen von Lunar Magic gebunden. Es ist auch möglich, den Code komplett nach seinen Vorstellungen zu verändern. Da Lunar Magic das aber nicht kann, brauch man dafür andere Programme. Im Falle von SMW benutzt man dafür meistens xkas, block tool oder sprite tool.
Auch block tool und sprite tool sind in gewisser Weise ziemlich limitiert, da sie den Code nur an einer festen Stelle in einer SMW ROM einfügen können. Mit xkas allerdings kann man Code an jeder beliebigen Stelle der ROM einfügen, daher ist xkas für ASM Patches auch am besten geeignet. Wie genau das funktioniert, erkläre ich euch im Laufe des Tutorials.
In SMW wird ASM Code meisten dafür verwendet, Adressen aus der RAM Map zu verändern. Diese Enthalten sämtliche Informationen über den Spielverlauf. Indem man diese Adressen verändert, kann man also auf den Spielverlauf Einfluss nehmen.
---------------------------------------------------------------------------
LEKTION 3: DER ACCUMULATOR UND DAS LADEN UND SPEICHERN VON WERTEN
Fangen wir erst mal mit einer der wichtigsten Begriffe der ASM Programmierung an, dem Accumulator. Der Accumulator ist ein so genanntes Register. Register sind vereinfacht gesagt Variablen, die bestimmte Zahlen enthalten und durch ASM Befehle (Opcodes genannt) verändert werden können. Der Accumulator ist das wichtigste aller Register. Mit ihm werden die meisten Operationen und Rechnungen durchgeführt. Es gibt viele Befehle, mit denen man den Accumulator beeinflussen kann. Fangen wir mal mit den leichtesten an.
LDA #10
Dieser Befehl lädt die Dezimalzahl 10 in den Accumulator.
LDA #%01001100
Dieser Befehl lädt die binäre Zahl 01001100 in den Accumulator.
Da man aber in ASM meistens mit Hexadezimalzahlen rechnet, sieht man diese Befehle eher selten. Viel häufiger sieht man da folgendes:
LDA #$1F
Lädt die Hexadezimalzahl 1F in den Accumulator.
Ihr solltet euch an diesesr Stelle also auf jeden Fall schon mal merken, dass man Hexdezimalzahlen immer durch ein $-Zeichen symbolisiert, also z.B. $10, $AB, $F3 usw.
Was fängt man aber nun mit diesen Zahlen an? Nun, man kann sie in Adressen aus der RAM Map speichern. Das funktioniert z.B. so:
STA $7E0019
Dies speichert die Zahl im Accumulator in RAM Adresse $7E0019. Schauen wir mal in der RAM Map nach, wofür diese Adresse gut ist.
Aha. Das ist also Marios Powerup. Indem wir einen der angegebenen Werte in diese Adresse speichern, können wir Mario's Powerup beeinflussen.
LDA #$02 ; Das hier ist übrigens ein Kommentar
STA $19
Kommentare stehen immer am Ende der Zeile, sind durch ein Semikolon abgetrennt und werden vom Programmcode ignoriert.
Dieser Code macht Mario also zu Cape Mario. War doch ganz schön einfach, oder? Aber halt mal, wieso habe ich einfach nur $19 geschrieben? Nun, es gibt bestimmte Register, die einem eine Menge Arbeit ersparen.
STA $19
STA $0019
STA $7E0019
Diese drei Befehle sind alle möglich und speichern den Wert im Akkumulator in RAM Adresse $7E0019. Dafür sorgen die so gennanten Direct Page- und Data Bank Register. Diese ersetzen bei Befehlen wie LDA, STA und noch vielen anderen die fehlenden Ziffern. Das Data Bank Register (DB) ist eine 8-Bit Zahl, die das High Byte (das Byte ganz links) ersetzt, wenn man es wg lässt. In SMW ist es fast immer $7E. LDA $0019 ist deshalb also gleichzusetzen mit LDA $7E0019. Und was ist das Direct Page Register? Das Direct Page Register (DP) ist ein 16-Bit Register, dass bei einem LDA Befehl zur Adresse hinzuaddiert wird. Beispiel: Ist das Direct Page Register $0200 und ihr benutzt den Befehl "LDA $19", so wird in Wirklichkeit die Adresse $0219 geladen. Ist das Direct Page Register $05, so bekommt ihr die Adresse $001E wenn ihr "LDA $19" benutzt. In SMW ist das Direct Page Register meistens $0000. Hier sind noch ein paar weitere Beispiele:
; DB: $7E, DP: $0000
LDA $19
; Adresse im Accumulator: $7E0019
; DB: $7E, DP: $0201
LDA $19
; Adresse im Accumulator: $7E021A
; DB: $3E, DP: $0000
LDA $05
; Adresse im Accumulator: $3E0005
; DB: $2E, DP: $0300
LDA $0A
; Adresse im Accumulator: $2E030A
Wie genau man das Data Bank- und das Direct Page Register beeinflusst, erkläre ich euch an einer anderen Stelle. Diese Register haben übrigens nur auf Adressen Einfluss. Also wenn ihr z.B. schreibt "LDA #$AF", so wird die Zahl $AF in den Accumulator geladen, unabhängig vom Data Bank- und Direct Page Register.
Ach und noch etwas:
STA $19 ($19 = 8-Bit Adresse) nennt man Direct Adressing
STA $0019 ($0019 = 16-Bit Adresse) nennt man Absolute Adressing
STA $7E0019 ($7E0019 = 24-Bit Adresse) nennt man Long Adressing
Übrigens kann man auch Adressen in den Accumulator laden. Also
LDA $19
LDA $0019
LDA $7E0019
sind alle drei möglich. Wäre Mario also gerade Cape Mario, so wäre nun der Wert $02 im Accumulator. Folgende Befehle sind nicht möglich (und währen auch ziemlich sinnlos):
STA #$19
STA #$0019
STA #$7E0019
Übrigens ist es in xkas Patches auch möglich, bestimmte Begriffe mit Werten zu verknüpfen. Dafür müsst ihr einfach an den Anfang des Patches schreiben:
!Powerup = $19
!ZufaelligeAdresse = $23
!NocheineAdresse = $50
[...]
Nun könnt ihr diese Begriffe ganz leicht in eurem Patch wiederverwenden:
LDA !Powerup ; = LDA $19
LDA #!Powerup ; = LDA #$19
LDA #!NocheineAdresse ; = LDA #$50
Beachtet, dass xkas zwischen Groß- und Kleinbuchstabe unterscheidet. Außerdem gibt es kein
!Begriff1 = #$19
Stattdessen schreibt ihr
!Begriff1 = $19
und dann nachher im Code
LDA #!Begriff1
Es gibt auch noch den Befehl STZ (Set to Zero), mit dem ihr eine eine Adresse direkt auf $00 setzen könnt. Also
STZ $19
entspricht
LDA #$00
STA $19
Beachtet, dass STZ nur in Verbindung mit 8- und 16-bit Adressen geht. Es gibt kein STZ $7E0019 oder ähnliches.
---------------------------------------------------------------------------
LEKTION 4: EINFACHE RECHENOPERATIONEN
Die einfachsten zwei Rechenbefehle (wenn man sie denn so nennen kann) sind INC und DEC. INC inkrementiert (erhöht) einen Wert um $01, DEC dekrementiert (verringert) einen Wert um $01. Beispiele:
LDA #$03
INC A ; Der Accumulator ist jetzt $04
LDA #$06
DEC A ; Der Accumulator ist jetzt $05
Das ganze funktioniert aber nicht nur mit dem Accumulator, sondern auch mit Adressen.
INC $19
inkrementiert RAM Adresse $19 um $01,
DEC $19
dekrementiert RAM Adresse $19 umd $01.
Das geht aber nur mit 8- und 16-bit Adressen. INC $7E0019 z.B. geht nicht, genau so wenig wie DEC $7E1DBF.
Während das ganze zwar schon ziemlich toll ist, wäre es doch schön, wenn man auch beliebige Zahlen addieren bzw. subtrahieren könnte, oder? Nun, es geht! Dafür gibt es die Befehle ADC (Add with Carry) und SBC (Subtract with Carry). Diese addieren bzw. subtrahieren eine bestimmte Zahl vom Accumulator. Allerdings ist etwas wichtiges zu beachten:
CLC
ADC #$03 ; Der Accumulator enthält jetzt den Wert $04
LDA #$09
SEC
SBC #$05 ; Der Accumulator enthält jetzt den Wert $04
Vor einer normalen Addition solltet ihr immer den Befehl CLC (Clear Carry Flag) und vor einer normalen Subtraktion den Befehl SEC (Set Carry Flag) schreiben. Wieso das so ist und mögliche Ausnahmen erkläre ich euch im nächsten Kapitel. Noch was wichtiges:
LDA #$00
SEC
SBC #$01
Der Accumulator enthält nun den Wert $FF.
LDA #$FF
CLC
ADC #$01
Der Accumulator enthält nun den Wert $00.
Ergibt eine Addition also einen Wert über $FF, so geht das ganze bei $00 weiter. Ergibt eine Subtraktion einen Wert unter $00, so geht das ganze bei $FF weiter.
---------------------------------------------------------------------------
LEKTION 5: DIE PROCESSOR FLAGS
Wenn es euch bis jetzt schwer gefallen ist diesem Tutorial zu folgen, solltet ihr noch mal die Zähne zusammenbeißen, denn hier wird es wieder ein bisschen abstrakt.
Also was sind Processor Flags? Processor Flags sind Bits der Hardware, die von bestimmten Befehlen unter bestimmten Umständen aktiviert werden. Die Processor Flags haben folgende Form:
envmxdizc
Jedes dieser Bits steht für eine Processor Flag. Abgesehen von der e Flag können alle Processor Flags mit dem Befehl REP gesetzt und mit SEP gecleart werden. Für einige Flags gibt es auch noch Sonderbefehle. Welche Befehle ihr genau für welche Flag braucht, erkläre ich euch an passender Stelle. Ein wichtiger Befehl für die Processor Flags ist CMP.
LDA #$03
CMP #$02
Dieser Befehl vergleicht eine Zahl mit dem Accumulator, indem er sie von ihm subtrahiert. Dabei werden allerdings nur die Processor Flags beeinflusst, nicht der Accumulator selbst. Wenn ihr das CMP ganz weg lässt, so wird automatisch immer mit $00 verglichen. Nun erkläre ich euch, was die Processor Flags im eizelnen tun und wofür sie nützlich sein können.
e - Emulation Mode
Diese Flag ist für SMW nicht so wichtig und ich verstehe nicht so viel davon, deswegen gehe ich auch nicht weiter darauf ein. Alles was ich weiß ist, dass das SNES, wenn dieses Bit clear ist, im Emulation Mode ist und wie ein NES funktioniert. Ist das Bit gesetzt, ist das SNES im Native Mode. Wie bereits erwähnt, kann man dieses Bit nicht mit REP oder SEP beeifnlussen. Die einzige Möglichkeit dieses Bit zu setzten oder zu clearen ist es mit dem c Bit (wird nachher erklärt) zu tauschen. Dafür gibt es den Befehl XCE. Mit CLC cleart man das c Bit und mit SEC setzt man das c Bit. Mit diesem code aktiviert man also den Emulation Mode:
CLC
XCE
Mit diesem Code aktiviert man den Native Mode
SEC
XCE
Da ein SNES leistungsfähiger als ein NES ist, wird man bei einer ROM so früh wie möglich in den Native Mode wechseln wollen.
n - Negative Flag
Die Negative Flag wird immer dann aktiviert, wenn irgendeine vorhergehende Operation als Ergebnis einen Wert über $80 (8-bit Modus) oder über $8000 (16-bit Modus) hat. Wieso ist das so? Nun ganz einfach. Muss muss sich nur mal die Zahlen binär angucken.
$80 = %10000000
In vielen Situationen (zum Beispiel bei der Geschwindigkeit von Sprites) ist es so, dass es sehr nützlich wäre, wenn man auch negative Wert angeben könnte. Darum hat man sich gesagt, dass das höchste Bit (in diesem Fall Bit 7) das Vorzeichen darstellt. 0 = +, 1 = -. So einfach ist das! Alle Wert über $80 sind Minus-Werte! Darum wird die Negative Flag bei Werten über $80 bzw. über $8000 gesetzt. Manuell kann man die Negative Flag mit SEP #$80 setzen und mit REP #$80 clearen. Die Flag wird übrigens auch durch LDA beeinflusst. Also
LDA #$91 ; Irgendeine Zahl über $80
setzt die Negative Flag, während
LDA #$45 ; Irgendeine Zahl unter $80
sie cleart.
v - Overflow Flag
Wird gesetzt, wenn man eine Zahl zwischen $80 und $FF zum Accumulator hinzuaddiert und gecleart, wenn man eine Zahl zwischen $80 und $FF vom Accumulator subtrahiert.
LDA #$03
CLC
ADC #$83
setzt die Overflow Flag,
LDA #$03
SEC
SBC #$91
cleart die Overflow Flag.
Die Overflow Flag kann man manuell mit SEP #$40 setzen und mit REP #$40 clearen.
m - Accumulator Size Flag
Dieses Bit aktiviert man mit SEP #$20 und cleart es mit REP #$20. Es legt die Größe des Accumulators fest. Ist es gesetzt, hat der Accumulator eine Größe von 8-bit, andernfalls hat er eine Größe von 16-bit. Im 8-bit Modus kann der Accumulator Zahlen von $00 bis $FF enthalten. Im 16-bit Modus kann er Zahlen von $0000 bis $FFFF enthalten. Wenn der Accumulator 16-bit groß ist nennt man das linke Byte "High Byte" und das rechte Byte "Low Byte". Speichert man einen 16-bit Accumulator in eine Adresse, so wird auch die nachfolgende Adresse betroffen. Dabei wird in die angegebene Adresse das Low Byte und in die nachfolgende Adresse das High Byte gespeichert.
Beispiel:
LDA #$13AF
STA $1DB9
Nach diesem Befehl enthält die Adresse $1DB9 den Wert $AF und die Adresse $1DBA den Wert $13. Mit dem Laden geht es genau so.
Achtung! Seid ihr im 16-bit und ladet eine 8-bit Zahl, wird das wahrscheinlich unvorhersehbare Folgen haben. Selbiges gilt, wenn ihr im 8-bit Modus seid und eine 16-bit Zahl ladet. Also Beispiel:
REP #$20
LDA #$FF
oder
SEP #$20
LDA #$FFFF
Diese Codes führen beide ins Chaos! Außerdem sollten ihr nicht vergessen, das Bit wieder zu setzen, wenn ihr es in einem Patch gecleart hat (in SMW ist es die meiste Zeit lang gesetzt).
x - Index Size Flag
Ist genau wie die Accumulator Size Flag, bloß, dass sie die Größe der Register X und Y bestimmt. Mehr zu diesen Registern in einem anderen Kapitel. Dieses Bit wird mit SEP #$10 gesetzt und mit REP #$10 gecleart.
d - Decimal Flag
Ist dieses Bit gesetzt, werden Rechnungen dezimal durchgeführt. Beispiel:
LDA #$06
CLC
ADC #$06 ; Der Accumulator enthält jetzt den Wert $12, nicht etwa $0C
Setzen kann man dieses Bit entweder mit SEP #$08 oder mit dem Befehl SED. Clearen kann man dieses Bit entweder mit REP #$08 oder mit CLD.
i - Interrupt Disable Flag
Diese Flag kann Interrupts wie IRQ deaktivieren (allerdinsg kein NMI). Mehr dazu in einem anderen Kapitel... Vielleicht...
Kann mit SEP #$04 oder SEI gesetzt und mit REP #$04 oder CLI gecleart werden.
z - Zero Flag
Wird gesetzt, wenn eine vorhergehende Operation $00 ergibt. Also:
LDA #$03
SEC
SBC #$03
setzt die Zero Flag, aber auch
LDA #$FF
CLC
ADC #$01
setzt die Zero Flag. Kommt bei einer Rechnung nicht $00 heraus, wird die Zero Flag gecleart.
c - Carry Flag
Diese Flag wird immer dann gesetzt, wenn bei einer Addition ein Wert über $FF (bzw. $FFFF im 16-bit Modus) herauskommt und dann gecleart, wenn bei einer Subtraktion ein Wert unter $00 herauskommt. Es gibt auch andere Situationen, in denen die Carry Flag beeinflusst wird. Aber was bringt sie überhaupt?
Ich habe ja irgendwo oben erwähnt, dass man ADC immer in Kombination mit CLC und SBC immer in Kombination mit SEC verwenden soll. SEC setzt die Carry Flag, während CLC sie cleart. Bei ADC ist es in Wirklichkeit so, dass nicht nur die Zahl hinter ADC zum Accumulator hinzuaddiert wird, sondern auch die Carry Flag. Bei SBC ist es so, dass zusätzlich #$01 subtrahiert wird, wenn die Carry Flag clear ist. Ziemlich schwachsinnig, oder? Nun, nicht unbedingt! Es gibt auch Situationen, wo das für uns ziemlich nützlich sein kann!
Stellt euch vor ihr wollt einen Münzcounter mit 6 Stellen machen. Der Accumulator kann aber maximal Zahlen bis $FFFF (also 65535) enthalten. Alleine mit dem Accumulator ist das ganze also nicht möglich. Mit der Carry Flag geht das aber! Nehmen wir einmal an, dass die Adressen $7F0D00, $7F0D01 und $7F0D02 die Daten für den Münz Counter enthalten. Maximal wäre also ein Wert von $FFFFFF, 16777215 in dezimal, möglich. Sagen wir $7F0D02 wäre das High Byte und $7F0D00 das Low Byte. Auf folgende Weise kann man den Münz Counter realisieren:
REP #$20
LDA $7F0D00
CLC
ADC #$01
STA $7F0D00
SEP #$20
LDA $7F0D02
ADC #$00
STA $7F0D02
Was genau macht dieser Code? Nun, zu erst mal wechseln wir mit REP #$20 in den 16-Bit Modus und laden die Adressen $7F0D00 und $7F0D01 in den Accumulator. Danach clearen wir die Carrly Flag und addieren $01 zum Accumulator hinzu. Stellt euch vor im Accumulator wäre nun die Zahl $FFFE. Wir addieren $01 hinzu, die Zahl ist nun $FFFF. Wir speichern diesen Wert wieder in $7F0D00. Danach gehen wir zurück auf den 8-Bit Modus, laden $7F0D02 und addieren $00 hinzu. Nichts passiert. Wir speichern den Accumulator wieder in $7F0D02 ab.
Nun stellt eucht vor ihr führt genau den selben Code noch einmal aus. Was passiert? Da $7F0D00 vorher $FFFF enthielt und ihr nun $01 hinzuaddiert, enthält $7F0D00 anschließend $0000, außerdem wird die Carry Flag gesetzt. Da ihr anschließend nicht die Carry Flag cleart, wird zu $7F0D02 zusätzlich $01 hinzuaddiert. Hatte der Münzcounter also vorher noch den Wert $00FFFF, enthält er jetzt den Wert $010000. Ziemlich praktisch, oder?
Die Carry Flag kann man auch noch mit SEP #$01 setzen und mit REP #$01 clearen.
So! Das war erst mal meine Einführung zu den Processor Flags. Zu abstrakt? Das muss aber sein, wenn man ASM wirklich verstehen will! Warum seht ihr in der nächsten Lektion.
---------------------------------------------------------------------------
LEKTION 6: BRANCHES UND SUBROUTINEN
Wie ihr sicherlich gemerkt habt, sind "LDA" und "STA" schon ganz toll. Mit diesen Befehlen alleine kann man allerdings noch keinen komplizierten Code schreiben. Es muss also irgendwie möglich sein, einen Code dynamisch zu schreiben, damit es auf verschiedene Situationen auch verschieden reagieren kann. Dafür gibt es so genannte "Branches". Gleich werdet ihr auch verstehen, was die Processor Flags mit dem ganzen zu tun haben.
Erst mal: Was sind Branches überhaupt? Nun "Branch" heißt übersetzt "Zweig". Branches gibt es in wirklich jeder Programmiersprache, nur heißen sie meistens anders (z.B. "If Case" oder "Condition"). Vereinfacht ausgedrückt überprüfen Branch Befehle den Status bestimmter Processor Flags und führen daraufhin einen von zwei möglichen Codes aus. Der allgemeine Aufbau ist dabei wie folgt:
[BRANCH BEFEHL] Label
[BEFEHL] ;\
[BEFEHL] ; | FALL 1 (BEDINGUNG NICHT ERFÜLLT)
[BEFEHL] ;/
[...]
Label:
[BEFEHL] ;\
[BEFEHL] ; | FALL 2 (BEDINGUNG ERFÜLLT)
[BEFEHL] ;/
[...]
Das ist der grundlegende Aufbau der meisten Branch Befehle. Ganz oben steht der Branch Befehl, der eine Bedinung überprüft. Ist diese Bedingung erfüllt, so wird der in diesem Beispiel als FALL 1 betitelte Code übersprungen und direkt der Code unter dem Label (hier FALL 2) ausgeführt. Ist die Bedingung nicht erfüllt, so wird der Code unter dem Branch Befehl (hier FALL 1) ausgeführt. Beachtet allerdings, das danach trotzdem noch der unter dem Label stehende Code (also FALL 2) ausgeführt wird. Der Label kann übrigens ein x-beliebiger Name sein. Ihr müsst nur sicherstellen, dass er keine Leerzeichen enthält und dass ihr zwei mal den gleichen Namen verwendet. Also ihr könntet euren Label auch "BedingungErfuellt" nennen. Dann müsstet ihr statt "Label:" aber auch "BedingungErfuellt:" benutzen. Und beachtet unbedingt, dass xkas zwischen Groß- und Kleinschreibung unterscheidet. "label" und "Label" sind also nicht das selbe.
Es gibt noch andere Verwendungen für Branch Befehle, nämlich so genannte "Loops" oder "Schleifen". Der Aufbau ist ähnlich wie bei normalen Labels, allerdings rückwärts. Beispiel:
Label:
[BEFEHL] ;\
[BEFEHL] ; | FALL 1 (BEDINGUNG ERFÜLLT)
[BEFEHL] ;/
[...][BRANCH BEFEHL] Label
[BEFEHL] ;\
[BEFEHL] ; | FALL 2 (BEDINGUNG NICHT ERFÜLLT)
[BEFEHL] ;/
[...]
Was macht dieser Code? Nun, zuerst wird der "FALL 1" Code ausgeführt, danach wird die Bedingung überprüft. Was passiert dann? Nun, wenn die Bedingung erfüllt ist, wird rückwärts im Code gesprungen. Das heißt der "FALL 1" Code wird erneut ausgeführt. Danach wird die Bedingung erneut überpüft. Ist sie wieder erfüllt, wird wieder der "FALL 1" Code ausgeführt. Das wiederholt sich dann so lange, bis die Bedingung nicht mehr erfüllt ist. Erst dann wird der "FALL 2" Code ausgeführt. Dieser Aufbau ist also nützlich, wenn ihr einen bestimmten Code x mal ausführen wolt. Ihr solltet allerdings aufpassen, dass ihr keine Endlos-Schleife kreiert, da sich das Spiel sonst aufhängt.
Im Spziellen gibt es nun folgende Branch Befehle (rechts daneben immer die Bedingung):
BEQ (Branch if Equal): Springt, wenn die Zero Flag gesetzt ist
BNE (Branch if not Equal): Springt, wenn die Zero Flag clear ist
BCC (Branch if Carry clear): Springt, wenn die Carry Flag gesetzt ist
BCS (Branch if Carry set): Springt, wenn die Carry Flag clear ist
BMI (Branch if Minus): Springt, wenn die Negative Flag gesetzt ist
BPL (Branch if Plus): Springt, wenn die Negative Flag clear ist
BVS (Branch if Overflow set): Springt, wenn die Overflow Flag gesetzt ist
BVC (Branch if Overflow clear): Springt, wenn die Overflow Flag clear ist
BRA (Branch always (8-bit)): Springt immer
BRL (Branch always long (16-bit)): Springt immer
OK... Aber was nützt uns das ganze jetzt? Nun an dieser Stelle ist vielleicht noch nicht klar, was das ganze Zeug mit den Processor Flags soll. Aber ihr werdet es nachher verstehen, wenn ich es euch erklärt habe. Ich fange mal mit den leichtesten Branch Befehlen an: BEQ und BNE.
BEQ springt, wenn die Zero Flag gesetzt ist. BNE springt, wenn die Zero Flag clear ist. Aber wann wird die Zero Flag denn überhaupt nochmal gesetzt? Nun, wir sollten uns hier an einen ganz wichtigen Befehl erinnern, der bei fast allen Branch Befehlen eine Rolle spielt: CMP. Wie war das nochmal? CMP subtrahiert virtuell eine Zahl von Accumulator, beeinflusst dabei aber in Wirklichkeit nur die Processor Flags. Und wann ist die Zero Flag nochmal gesetzt? Wenn das Ergebnis einer Operation $00 ergibt. Und wann passiert das? Nun, jetzt sind wir genau da angekommen, worauf ich hinaus wollte!
LDA #$02
CMP #$02
Zero Flag = Gesetzt, da $02 - $02 = $00
LDA #$7A
CMP #$7A
Zero Flag = Gesetzt, da $7A - $7A = $00
LDA #$00
Zero Flag = Gesetzt, da $00 - $00 = $00
Wie schon mal erwähnt, kann man das "CMP #$00" einfach weg lassen.
LDA #$03
CMP #$04
Zero Flag = Clear, da $03 - $04 = $FF
Aaaaaaaah! Dafür sind BEQ und BNE also gut! BEQ springt also immer dann, wenn zwei Zahlen gleich sind, während BNE springt, wenn zwei zahlen ungleich sind. Und um herauszufinden, wann das der Fall ist, werden die Processor Flags benutzt. Auf einmal ergibt alles einen Sinn! Allerdings gibt es noch mehr Situationen, in denen diese Befehle springen. Beispiel:
[...]
LDA #$FE
CLC
ADC #$02
BEQ Label1
[...]
Label1:
[...]
Auch in diesem Fall springt BEQ zu Label1, da $FE + $02 = $00 ist. Verständlich, oder? Mit diesem ganzen Vorwissen dürften auch die meisten anderen Branch Befehle nun viel leichter zu verstehen sein. Kommen wir also zu BCS und BCC.
BCS springt, wenn die Carry Flag gesetzt ist, BCC springt, wenn die Carry Flag clear ist. Wann passiert das noch mal? Auch hier müssen wir uns wieder an CMP erinnern. CMP subtrahiert eine Zahl vom Accumulator, wir müssen uns hier also nur auf die Subtraktion konzentrieren. Wir sagten, dass cie Carry Flag gecleart wird, wenn bei einer Subtraktion ein das Ergebnis kleiner als $00 ist und wieder bei $FF ankommt. Beispiel:
LDA #$02
CMP #$03
Carry Flag = Clear, da $02 - $03 = $FF
LDA #$05
CMP #$07
Carry Flag = Clear, da $05 - $07 = $FE
LDA #$04
SEC
SBC #$05
Carry Flag = Clear, da $04 - $05 = $FF
LDA #$04
CMP #$03
Carry Flag = Set, da $04 - $03 = $01
LDA #$04
CMP #$04
Carry Flag = Set, da $04 - $04 = $00
Mit BCC kann man also prüfen, ob eine Zahl kleiner ist als eine andere, während man mit BCS prüfen kann, ob eine Zahl größer oder gleich eine andere Zahl ist. Diese Befehle werdet ihr wahrscheinlich sehr häufig verwenden. Nehmen wir wieder Marios Powerup als Beispiel. Ihr wollt einen Block machen, der euch nur dann zu Feuer Mario macht, wenn ihr Small Mario oder Super Mario seid. Die RAM Adresse für Marios Powerup ist nach wie vor $19 und kann folgende Werte enthalten:
$00 - Small Mario
$01 - Super Mario
$02 - Cape Mario
$03 - Feuer Mario
Der Block soll euch also zu Feuer Mario machen, wenn Adresse $19 < $02 ist. Das lässt sich mit diesen Befehlen umsetzen. Eines sollte ich euch aber noch sagen: Wenn ihr mit Branches arbeitet, werdet ihr meistens den gegenteiligen Befehl von dem nehmen, den ihr eigentlich benutzen wollt. Hier nun ein Beispiel:
LDA $19 ; Lade das Powerup
CMP #$01 ; Vergleiche mit $01
BCS NichtFeuerMario ; Größer/gleich $01? Dann nicht zu Feuer Mario machen!
LDA #$03 ;\ Andernfalls mache Mario zu Feuer Mario
STA $19 ;/
NichtFeuerMario:
[...]
So z.B. könnte das ganze aussehen. Aber wieso wäre hier BCC nicht ganz so schön? Nun, das zeige ich euch gerne:
LDA $19 ; Lade das Powerup
CMP #$02 ; Vergleiche mit $02
BCC FeuerMario ; Kleiner $02? Dann mache Mario zu Feuer Mario
[...]
FeuerMario:
LDA #$03 ;\ Dieser Code wird immer ausgeführt
STA $19 ;/
Nun ist ganz leicht zu sehen, warum BCS hier eindeutig besser geeignet ist. Benutzt ihr BCC, so wird, wenn die Bedingung erfüllt ist, der Code unter "BCC" gar nicht ausgeführt. Anders wird aber der Code unter "FeuerMario:" selbst dann ausgefüllt, wenn die Bedingung nicht erfüllt ist. Zugegeben, dieses Problem ließe sich leicht beheben:
LDA $19 ; Lade das Powerup
CMP #$02 ; Vergleiche mit $02
BCC FeuerMario ; Kleiner $02? Dann mache Mario zu Feuer Mario
AndererCode:
[...]
BRA Ueberspringen
FeuerMario:
LDA #$03 ;\ Mache Mario zu Feuer Mario
STA $19 ;/
BRA AndererCode
Ueberspringen:
Dieser Code funktioniert genau wie der Code mit BCS, da "BRA" immer springt. Allerdings enthält er einige Befehle mehr (ist also minimal langsamer) und sieht auch einfach hässlicher aus. Ihr solltet euch also schon mal daran gewöhnen, bei Branch Befehlen etwas umzudenken. Am Anfang ist es aber noch normal, wenn man es auf die eben gezeigte Art und Weise macht.
Kommen wir zu den nächsten zwei Branch Befehlen: BMI und BPL.
Hier gibt es eigentlich nicht viel zu erzählen. BMI springt, wenn die Negative Flag gesetzt ist, also bei einer negativen Zahl. BPL hingegen springt, wenn die Negative Flag clear ist, also bei einer positivien Zahl. Darauf will ich nicht lange eingehen. Nur ein paar Beispiele:
LDA #$81
BMI
Negative Flag = Gesetzt, BMI springt
LDA #$10
BMI
Negative Flag = Clear, BMI springt nicht
LDA #$40
BPL
Negative Flag = Clear, BPL springt
LDA #$FF
BPL
Negative Flag = Gesetzt, BPL springt nicht.
Keine Ahnung, wo das nützlich sein könnte. Vielleicht bei der Programmierung von Sprites.
BVS springt dann, wenn die Overflow Flag gesetzt ist. BVC springt dann, wenn die Overflow Flag clear ist.
Ich kann mir echt nicht vorstellen, wo das nützlich sein könnte. Hier aber mal einige Beispiele:
LDA $03
CLC
ADC #$9A
BVS IrgendEinLabel
Overflow Flag = Gesetzt, BVS springt
LDA
SEC
SBC #$BC
BVC IrgendEinLabel
Overflow Flag = Clear, BVC springt
Ich denke darauf brauche ich nicht weiter einugehen.
Nun noch die letzten zwei Branch Befehle: BRA und BRL.
BRA und BRL springen immer. Dabei ist BRA 8-bit und BRL 16-bit. Wie jetzt, 8-bit und 16-bit? Ach stimmt ja, das habe ich ja noch gar nicht erwähnt!
Oben habe ich ja die ganze Zeit Labels verwendet. Das liegt daran, dass ich die ganze Zeit davon ausging, dass wir xkas benutzen. In Wirklichkeit gibt es im Programmcode von SMW aber keine Label. Branch Befehle geben nämlich nicht an, wohin sie springen sollen, sondern wie viele Bytes sie überspringen sollen. Wenn wir Labels verwenden, übersetzt xkas das ganze aber entsprechend. Außerdem sollte man wissen, dass der Wert hinter einem Branch Befehl immer ein signierter Wert ist. Das bedeutet, dass Zahlen von $80 bis $FF (bzw. von $8000 bis $FFFF) als negative Zahlen gedeutet werden. Muss ja so sein, denn sonst wären Loops überhaupt nicht möglich. Nun noch einige Beispiele dazu:
BEQ Label1
LDA #$03
STA $19
LDA #$04
STA $0DBE
Label1:
sieht in Wirklichkeit so aus:
BEQ $09
LDA #$03
STA $19
LDA #$04
STA $0DBE
Warum hier $09 hinkommt und nicht etwa $04, wie ihr vielleicht geglaubt habt, erkläre ich euch an einer anderen Stelle.
Label1:
LDA #$03
STA $19
LDA #$04
STA $0DBE
LDA $0DBF
BEQ Label1
sieht in Wirklichkeit aus so aus:
LDA #$03
STA $19
LDA #$04
STA $0DBE
LDA $0DBF
BEQ $8B
Ich hoffe mal, das wurde so einigermaßen verstanden. Ach ja, noch was:
BRA $00
tut überhaupt gar nichts.
Das war's dann soweit zu Branches. Allerdings möchte ich in dieser Lektion auch noch ein paar andere wichtige Funktionen erläutern, nämlich Jumps und Subroutinen.
Als aller erstes mal Jumps. Für Jumps gibt es die Befehle JMP (16-bit) und JML (24-bit). Sie funktionieren ähnlich wie BRA und BRL, haben aber einen entscheidenden Vorteil: Sie können nicht nur $80 bzw. $8000 Bytes überspringen, sondern an eine beliebige Stelle in der ROM springen. Darum kommt hinter diese Befehle auch nicht die Anzahl der Bytes, die ihr überspringen wollt, sondern die Adresse, zu der ihr springen wollt. Beispiel:
JML $248200
springt zu Adresse $2482000 in eurer ROM.
JMP $8200
springt zu Adresse $XX8200 in eurer ROM.
Das ganze kann ziemlich nützlich sein, wenn ihr xkas Patches schreibt. Aber das erkläre ich euch an einer anderen Stelle.
Nun gibt es aber sogar noch etwas viel nützlicheres: Nämlich Subroutinen.
Was sind Subroutinen? Was eine Routine ist, wisst ihr sicherlich, nämlich eine Ansammlung von Code mit einem bestimmten Spiel. Beispiel:
LDA #$03
STA $19
Das ist eine Routine, die Mario zu Feuer Mario macht.
Nun stellt ich vor, ihr habt eine Routine, die sehr häufig im Spiel aufgeführt wird. Beispiel: Die "Level End" Routine. Diese wird nach jedem Level ausgeführt. Nun gäbe es zwei Optionen. Entweder wir machen für jedes Level eine neue Level End Routine. Das würde aber sehr viel Speicherplatz verbrauchen. Deswegen entscheiden wir uns für die bessere Lösung: Subroutinen!
Um es mal einfach auszudrücken: Subroutinen sind Routinen, die von einer beliebigen Position in eurer ROM aus aufgerufen werden können und nachdem sie beendet wurden wieder an die Position zurück springen, von der aus sie aufgerufen wurden. Subroutinen werden mit JSR (16-bit) oder JSL (24-bit) aufgerufen. Mit RTS (16-bit) oder RTL (24-bit) kehrt man von einer Subroutine zurück. Nun versuche ich mal euch das ganze zu veranschaulichen.
LDA #$03
STA $19
JSL $248200
LDA #$04
STA $0DBE
org $248200
LDA #$00
STA $0DBF
RTL
Fangen wir mal oben an. Wir laden den Wert $03 und speichern ihn in Adresse $19. Was genau das bringt spielt bei diesem Beispiel keine Rolle. Nun kommen wir bei JSL an. Was passiert jetzt? Das Programm springt jetzt an Adresse $248200 in der ROM. org benutzen wir in xkas Patches um dem Programm zu sagen, dass wir an einer bestimmten Adresse Code einfügen wollen. org $248200 fügt also Adresse $248200 den Code
LDA #$00
STA $0DBF
RTL
Das habe ich aber nur gemacht, damit man leichter nachvollziehen kann, was passiert, denn jetzt wissen wir genau, was unter $248200 passiert, zu der wir soeben gesprungen sind. Als nächstes wird also der Wert $00 geladen und in Adresse $0DBF gespeichert. Dann treffen wir auf das RTL. Was passiert jetzt? Jetzt springen wir zurück an die Stelle, an der das JSL stand und führen den Code dahinter auf, laden also in diesem Fall $04 und speichern den Wert in Adresse $0DBE.
Habt ihr nun so einigermaßen verstanden, wie Subroutinen funktionieren? Klar, dieses Beispiel wäre ohne Subroutine tausend mal besser. Aber stellt euch vor ihr hättet eine Routine von über 1000 Bytes, die nach jedem Level ausgeführt wird. In dem Fall würde man wirklich eine Menge Speicherplatz (und Zeit) verschwenden, wenn man die Routine für jedes Level neu schreiben würde. In solchen Fällen sind Subroutinen also wirklich Pflicht. Schlauer Einsatz von Subroutinen erleichtert euch die Programmierung in ASM um einiges!
Ach ja, noch etwas: Custom Blocks sind IMMER Subroutinen. Daher muss am Ende von Custom Blocks immer RTS (block tool) oder RTL (BTSD) stehen. Glückwunsch! Nun seid ihr bereits in der Lage eure eigenen Custom Blocks zu programmieren!
---------------------------------------------------------------------------
SPEZIAL 1: PRAXISTEST 1
Nun kommen wir zur aller, aller wichtigsten Lektion in Sachen ASM. Wer diese Lektion nicht beachtet, wird niemals erfolgreich in ASM programmieren können. Dabei ist sie so leicht! Sie lautet:
NICHT DURCH TUTORIALS LERNT MAN ASM, SONDERN DURCH AUSPROBIEREN!
Und da man sich zu so etwas aber ziemlich schwer durchringen kann, stelle ich euch hier ein paar Aufgaben, die ihr bewältigen solltet, bevor ihr euch an die nächste Lektion begebt.
-Erstellt einen Custom Block, der eure Münzen um 1 erhöht.
-Erstellt einen Custom Block, der eure Münzen nur dann um 1 erhöht, wenn ihr weniger als 99 (dezimal) Münzen habt und eure Münzen ansonsten auf 0 setzt.
-Erstellt einen Custom Block, der eure Leben um 1 erhöht, wenn ihr Feuer Mario seid.
-Erstellt einen Custom Block, der euch zu Cape Mario macht, wenn ihr 30 (dezimal) oder mehr Münzen habt und eure Münzen danach auf 0 setzt.
-Erstellt einen Custom Block, der euch zu Cape Mario macht, wenn ihr genau 0 Münzen habt.
-Erstellt einen Custom Block, der euch zu Cape Mario macht, wenn ihr nicht genau 0 Münzen habt.
-Erstellt einen Custom Block, der eure Münzen so lange um 1 erhöht, bis ihr genau 50 (dezimal) habt. Beachtet dabei, dass die Münzen nicht über 99 (dezimal) gehen dürfen).
-Erstellt einen Custom Block, der mit JSR zu einer Subroutine springt, die überprüft, ob ihr 50 (dezimal) oder mehr Münzen habt und in diesem Falle eure Münzen auf 0 setzt. Danach soll sie zur Hauptroutine zurück kehren.
Hiermit sei euch noch mal die RAM Map von SMW Central an's Herz gelegt. Da findet ihr eigentlich alles, was ihr für die Bewältigung dieser Aufgaben benötigt.
Könnt ihr diese Aufgaben alle blind bewältigen? Dann seid ihr bereit für die nächste Lektion!
---------------------------------------------------------------------------
LEKTION 7: INDEXING
Kommen wir nun zu einer der, wie ich finde, nützlichsten Funktionen in ASM, wenn man denn in er Lage ist sie zu meistern. Ich rede vom Indexing.
Ziemlich am Anfang habt ihr den Akkumulator (oder "A") als ein Register kennengelernt, mit dem man verschiedene Rechnungen durchführen und noch viel mehr anstellen kann. Nun möchte ich euch zwei Register vorstellen, die dem Akkumulator sehr ähnlich sind, jedoch noch ein paar Zusatzfunktionen haben und dafür ein paar Dinge nicht können, die der Akkumulator kann. Ich rede von den X- und Y Registern, auch "Index Register" genannt.
Viele der Befehle, die es für den Akkumulator gibt, gibt es auch für die X- und Y Register. Z.B. gibt es LDX und LDY zum laden von Werten und Adressen, STX und STY zum Speichern der Werte in Adressen, INX und INY bzw. DEX und DEY zum erhöhen bzw. verringern der Register, CPX und CPY zum Vergleichen der Register mit einer Zahl und sogar noch viele mehr. Das alles ist aber nur nebensächlich. Was diese Register viel interessanter macht ist das so genannte Indexing.
Stellt euch vor ihr wolltet einen Block machen, der abhängig von eurem Powerup verschiedene Routinen ausführt. Sagen wir einfach mal er soll eure Münzen um eine je nach Powerup variierende Anzahl erhöhen:
Small Mario - 10 Münzen
Super Mario - 25 Münzen
Cape Mario - 35 Münzen
Feuer Mario - 50 Münzen
Nach unserem bisherigen Wissen sollte das in etwa so aussehen:
LDA $19
CMP #$00 ; Powerup nicht 0? Mario nicht klein!
BNE Nichtklein
LDA #$10
BRA Addieren
Nichtklein:
CMP #$01 ; Powerup nicht 1? Mario nicht Super Mario!
BNE NichtSuperMario
LDA #$25
BRA Addieren
NichtSuperMario:
CMP #$02 ; Powerup nicht 2? Mario nicht Cape Mario!
BNE NichtCapeMario
LDA #$35
BRA Addieren
NichtCapeMario: ; Dann kann Mario höchstens noch Feuer Mario sein
LDA #$50
Addieren:
CLC
ADC $0DBF
STA $0DBF
Wie ihr seht, ist das schon ganz schön viel Schreibarbeit. Nun stellt euch mal vor ihr hättet nicht 4 verschiedene Werte, sondern 100. Da sähe die Sache nochmal ganz anders aus. Weil das wohl auch den Programmierern von damals zu blöd war, erfand irgendeiner schlauer Kopf das Indexing, das einem eine Menge Arbeit erspart. Hier nun der obige Code nochmal, bloß mit Indexing:
LDX $19
LDA MuenzTabelle,x
CLC
ADC $0DBF
STA $0DBF
MuenzTabelle:
db $10,$25,$35,$50
Woah! Das sieht doch schon mal wesentlich besser aus, nicht wahr? Nun mal zu Erläuterung. Als erstes mal sollte man alle in Frage kommenden Werte in einer Tabelle festhalten. In ASM gibt es verschiedene Formen von Tabellen, in diesem Beispiel wird die Tabelle durch "db" eingeleitet. Dahinter stehen die einzelnen Werte der Tabelle, die jeweils mit Kommata abgetrennt sind. Bitte merkt euch diesen Aufbau genau. Zuerst der Tabellentyp (hier "db"), dann ein Leerzeichen, dann die einzelnen Werte, jeweils durch Kommata abgetrennt. Hinter den Kommatas dürfen keine Leerzeichen stehen und hinter dem letzten Wert darf kein Komma stehen. Andere Tabellentypen sind zum Beispiel:
16BitTabelle:
dw $0000,$0002,$3456,$7895,$AAFF
24BitTabelle:
dl $700360,$700366,$70036A
In diesen Beispielen haben die Werte einfach nur verschiedene Längen. Ihr braucht euch aber nur "db" zu merken. Im Grunde genommen sind db, dw und dl sowieso alle genau gleich und sollen den Programmcode nur übersichtlicher machen. Werden solche Tabellen in eine ROM eingefügt, werden einfach nur die einzelnen Bytes in der selben Reihenfolge in die ROM eingefügt. Also nehmen wir einfach mal diese Tabelle:
TestTabelle1:
db $00,$01,$02,$03,$04,$05
Fügen wir diesen Code in einer ROM an einer bestimmten Stelle ein (zum Beispiel mit xkas), so würde an dieser Stelle dann in Hex stehen:
...00 01 02 03 04 05...
Dasselbe Ergenbis würde man mit folgenden Tabellen erreichen (auch bei Tabellen stehen die niederwertigeren Bytes immer vorne):
TestTabelle2:
dw $0100,$0302,$0504
TestTabelle3:
dl $020100,$050403
Bei manchen Assemblern, wie zum Beispiel Trasm, welcher von sprite tool benutzt wird, weichen die Tabellenbezeichnungen geringfügig ab. So verwendet man z.B. statt "db" in Trasm "dcb" oder statt "dw" dann "dcw".
Also ich hoffe mal ihr versteht so einigermaßen das Prinzip hinter Tabellen. Aber nun zurück zum eigentlichen Code. Mit der Tabelle alleine können wir ja noch nicht viel anfangen, erstmal müssen wir indexen. Hier kommen jetzt die Index Register ins Spiel.
LDX $19
LDA MuenzTabelle,x
[...]
Was LDX $19 tut wissen wir bereits: Es lädt den Wert der Adresse $19 in das X Register. Wirklich neu ist nur das LDA MuenzTabelle,x. Dieser Befehl lädt den x-ten Wert der Tabelle "MuenzTabelle" in den Akkumulator. Was genau heißt das jetzt? Nun, wir haben die Adresse $19 in unser X Register geladen. Dies ist, wie ihr wisst, Marios Powerup. Hier noch mal die genauen Werte:
$00 = Klein
$01 = Super Mario
$02 = Cape Mario
$03 = Feuer Mario
Stellen wir uns nun vor Mario ist klein. In dem Fall wird also der 0. Wert der MuenzTabelle in den Akkumulator geladen. Da wir bei Computern immer bei 0 anfangen zu zählen, laden wir also eine $10 in den Akkumulator. Ist Mario hingegen Super Mario, laden wir den 1. Wert, also $25 in den Akkumulator. Bei Cape Mario entsprechend $35 und bei Feuer Mario $50. So einfach geht das und es verkürzt euren Code in bestimmten Fällen ungemein. Das ganze geht aber auch mit RAM Adressen und wird sogar im Spiel so genutzt. Stellt euch nun vor ihr macht einen Patch für zwei Spieler. Natürlich soll jeder Spieler seine eigenen Adressen haben, aber ihr wollt auch nicht jede Funktion für jeden Spieler extra programmieren. Hier ist das Indexing sehr nützlich. Hier mal ein Beispiel direkt aus SMW:
$0DB3 = Der momentane Spieler; $00 = Mario, $01 = Luigi
$0DB4 = Marios Leben
$0DB5 = Luigis Leben
$0DBE = Leben des momentanen Spielers
Stellt euch vor ihr seid gerade am Ende eines Levels und wollt, dass eure Anzahl an Leben aus Adresse $0DBE in die dafür vorgesehene Adresse für den jeweiligen geschrieben wird. Das geht durch Indexing ganz leicht, denn auch für das Speicher von Werten gibt es einen Indexing Befehl:
LDX $0DB3 ; Anzahl an Spieler in X laden
LDA $0DBE ; Anzahl Leben in A laden
STA $0DB4,x ; Und in $0DB4 + x speichern
Dies funktioniert im Prinzip genau wie mit dem Laden, bloß andersherum. Ihr lädt den aktuellen Spieler in X und die Anzahl an Leben in $0DBE. Nun müsst ihr euch einfach vorstellen, dass unter $0DB4 eine Tabelle sein, in der ihr den Wert speicher wollt. Seid ihr Mario und ist das X Register somit $00, wird eure Anzahl an Leben an 0. Stelle, also in Adresse $0DB4 gespeichert. Seid ihr Luigi und ist das X Register somit $01, so wird die Anzahl an Leben an 1. Stelle gespeichert, also in $0DB5.
Vielleicht blickt ihr bei dem ganzen noch nicht so wirklich durch und findet es ziemlich kompliziert, aber macht euch da mal keine Gedanken. Das ist am Anfang völlig normal und reine Probiersache. Irgendwann habt ihr den Dreh dann raus und seid froh, dass es diese Tabellen und Indexing gibt.
Ach ja noch eine Kleinigkeit: Oben habe ich die ganze Zeit das X Register verwendet, aber mit dem Y Register geht das natürlich genauso. Lediglich eine kleine Einschränkung ist zu beachten. Während
STA $19,x
STA $0019,x
STA $7E0019,x
allesamt möglich sind, gibt es beim Y Register nur
STA $19,y
STA $0019,y
und kein "STA $7E0019,y". In der Regel solltet ihr also das X Register benutzen. Manchmal werdet ihr allerdings mit beiden arbeiten müssen. Außerdem solltet ihr wissen, dass ihr die Größe der Index Register ähnlich wie beim Akkumulator verändern könnt (was ja schon in der Lektion mit den Processor Flags angekratzt wurde). Mit REP #$10 stellt ihr die Größe der Index Register auf 16-bit, während ihr sie mit SEP #$10 wieder auf 8-bit stellt. Benutzt ihr REP #$30 und SEP #$30, so könnt ihr die Akkumulatorgröße und die Größe der Index Register gleichzeitig verändern.
Mit das quadratische Rad neu erfinden (englisch Reinventing the square wheel) bezeichnet man die Bereitstellung einer schlechten Lösung, wenn eine gute Lösung bereits existiert.
-Slowsort-
Slowsort (von engl. slow: langsam) ist ein langsamer, rekursiver Sortieralgorithmus, der nach dem Prinzip Vervielfache und kapituliere (engl. Multiply and surrender, eine Parodie auf Teile und herrsche) arbeitet.










